Abstract ring. More...
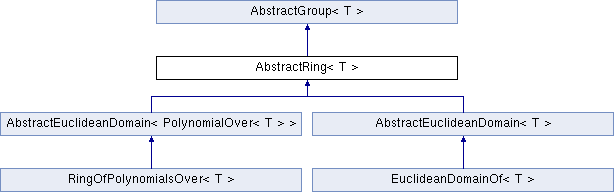
 Inheritance diagram for AbstractRing< T >:
Inheritance diagram for AbstractRing< T >:Public Types | |
| typedef T | Element |
 Public Types inherited from AbstractGroup< T > Public Types inherited from AbstractGroup< T > | |
| typedef T | Element |
Public Member Functions | |
| AbstractRing () | |
| Construct an AbstractRing. | |
| AbstractRing (const AbstractRing &source) | |
| Copy construct an AbstractRing. More... | |
| AbstractRing & | operator= (const AbstractRing &source) |
| Assign an AbstractRing. More... | |
| virtual bool | IsUnit (const Element &a) const =0 |
| Determines whether an element is a unit in the group. More... | |
| virtual const Element & | MultiplicativeIdentity () const =0 |
| Retrieves the multiplicative identity. More... | |
| virtual const Element & | Multiply (const Element &a, const Element &b) const =0 |
| Multiplies elements in the group. More... | |
| virtual const Element & | MultiplicativeInverse (const Element &a) const =0 |
| Calculate the multiplicative inverse of an element in the group. More... | |
| virtual const Element & | Square (const Element &a) const |
| Square an element in the group. More... | |
| virtual const Element & | Divide (const Element &a, const Element &b) const |
| Divides elements in the group. More... | |
| virtual Element | Exponentiate (const Element &a, const Integer &e) const |
| Raises a base to an exponent in the group. More... | |
| virtual Element | CascadeExponentiate (const Element &x, const Integer &e1, const Element &y, const Integer &e2) const |
| TODO. More... | |
| virtual void | SimultaneousExponentiate (Element *results, const Element &base, const Integer *exponents, unsigned int exponentsCount) const |
| Exponentiates a base to multiple exponents in the Ring. More... | |
| virtual const AbstractGroup< T > & | MultiplicativeGroup () const |
| Retrieves the multiplicative group. More... | |
 Public Member Functions inherited from AbstractGroup< T > Public Member Functions inherited from AbstractGroup< T > | |
| virtual bool | Equal (const Element &a, const Element &b) const =0 |
| Compare two elements for equality. More... | |
| virtual const Element & | Identity () const =0 |
| Provides the Identity element. More... | |
| virtual const Element & | Add (const Element &a, const Element &b) const =0 |
| Adds elements in the group. More... | |
| virtual const Element & | Inverse (const Element &a) const =0 |
| Inverts the element in the group. More... | |
| virtual bool | InversionIsFast () const |
| Determine if inversion is fast. More... | |
| virtual const Element & | Double (const Element &a) const |
| Doubles an element in the group. More... | |
| virtual const Element & | Subtract (const Element &a, const Element &b) const |
| Subtracts elements in the group. More... | |
| virtual Element & | Accumulate (Element &a, const Element &b) const |
| TODO. More... | |
| virtual Element & | Reduce (Element &a, const Element &b) const |
| Reduces an element in the congruence class. More... | |
| virtual Element | ScalarMultiply (const Element &a, const Integer &e) const |
| Performs a scalar multiplication. More... | |
| virtual Element | CascadeScalarMultiply (const Element &x, const Integer &e1, const Element &y, const Integer &e2) const |
| TODO. More... | |
| virtual void | SimultaneousMultiply (Element *results, const Element &base, const Integer *exponents, unsigned int exponentsCount) const |
| Multiplies a base to multiple exponents in a group. More... | |
Detailed Description
template<class T>
class AbstractRing< T >
Abstract ring.
- Template Parameters
-
T element class or type
const Element& returned by member functions are references to internal data members. Since each object may have only one such data member for holding results, the following code will produce incorrect results:
abcd = group.Add(group.Add(a,b), group.Add(c,d));
But this should be fine:
abcd = group.Add(a, group.Add(b, group.Add(c,d));
Constructor & Destructor Documentation
◆ AbstractRing()
|
inline |
Copy construct an AbstractRing.
- Parameters
-
source other AbstractRing
Member Function Documentation
◆ operator=()
|
inline |
Assign an AbstractRing.
- Parameters
-
source other AbstractRing
◆ IsUnit()
|
pure virtual |
Determines whether an element is a unit in the group.
- Parameters
-
a the element
- Returns
- true if the element is a unit after reduction, false otherwise.
Implemented in ModularArithmetic, GFP2_ONB< F >, RingOfPolynomialsOver< T >, GF2NP, QuotientRing< T >, QuotientRing< EuclideanDomainOf< PolynomialMod2 > >, and EuclideanDomainOf< T >.
◆ MultiplicativeIdentity()
|
pure virtual |
Retrieves the multiplicative identity.
- Returns
- the multiplicative identity
Implemented in GFP2_ONB< F >, RingOfPolynomialsOver< T >, MontgomeryRepresentation, ModularArithmetic, QuotientRing< T >, QuotientRing< EuclideanDomainOf< PolynomialMod2 > >, and EuclideanDomainOf< T >.
◆ Multiply()
|
pure virtual |
Multiplies elements in the group.
- Parameters
-
a the multiplicand b the multiplier
- Returns
- the product of a and b
Implemented in MontgomeryRepresentation, ModularArithmetic, GFP2_ONB< F >, RingOfPolynomialsOver< T >, GF2NT233, GF2NT, QuotientRing< T >, QuotientRing< EuclideanDomainOf< PolynomialMod2 > >, and EuclideanDomainOf< T >.
◆ MultiplicativeInverse()
|
pure virtual |
Calculate the multiplicative inverse of an element in the group.
- Parameters
-
a the element
Implemented in MontgomeryRepresentation, ModularArithmetic, GFP2_ONB< F >, RingOfPolynomialsOver< T >, GF2NT, QuotientRing< T >, QuotientRing< EuclideanDomainOf< PolynomialMod2 > >, and EuclideanDomainOf< T >.
◆ Square()
|
virtual |
Square an element in the group.
- Parameters
-
a the element
- Returns
- the element squared
Reimplemented in RingOfPolynomialsOver< T >, GF2NT233, GF2NT, QuotientRing< T >, QuotientRing< EuclideanDomainOf< PolynomialMod2 > >, and EuclideanDomainOf< T >.
Definition at line 37 of file algebra.cpp.
◆ Divide()
|
virtual |
Divides elements in the group.
- Parameters
-
a the dividend b the divisor
- Returns
- the quotient
Reimplemented in RingOfPolynomialsOver< T >, and EuclideanDomainOf< T >.
Definition at line 42 of file algebra.cpp.
◆ Exponentiate()
|
virtual |
Raises a base to an exponent in the group.
- Parameters
-
a the base e the exponent
- Returns
- the exponentiation
Definition at line 316 of file algebra.cpp.
◆ CascadeExponentiate()
|
virtual |
TODO.
- Parameters
-
x first element e1 first exponent y second element e2 second exponent
- Returns
- TODO
Definition at line 323 of file algebra.cpp.
◆ SimultaneousExponentiate()
|
virtual |
Exponentiates a base to multiple exponents in the Ring.
- Parameters
-
results an array of Elements base the base to raise to the exponents exponents an array of exponents exponentsCount the number of exponents in the array
SimultaneousExponentiate() raises the base to each exponent in the exponents array and stores the result at the respective position in the results array.
SimultaneousExponentiate() must be implemented in a derived class.
- Precondition
COUNTOF(results) == exponentsCount-
COUNTOF(exponents) == exponentsCount
Definition at line 334 of file algebra.cpp.
◆ MultiplicativeGroup()
|
inlinevirtual |
The documentation for this class was generated from the following files: